Gregory Vincent St. Thomasino:

I Googled “mathematical poetry” and I was not at all surprised to see my number one hit was your blog, Mathematical Poetry.

Your engagement with mathematical poetry, and with the aesthetics of the mathematical language, has been nothing short of inspired and is, I declare, historical. You seem to have found your niche, or else, and more important, a workable method. It will be helpful right now for our readers to know that for background information and for clarifications and to satisfy their curiosity they can visit Mathematical Poetry and they can visit your main website, The Art of Kaz Maslanka, to read and explore your theoretical writings and your commentaries and the many examples of your mathematical poetry and to discover the many sides to your artistic personality for you really are, in addition to being a mathematician, a true polyartist. (And there are, at the main website, two portraits of you--the one as a young man and then the one in a leather motorcycle jacket--that are absolutely priceless.)

Before we get down to business: I had the pleasure of your company recently and I want to say you are maybe the most intellectually generous person I have ever met; you are both aware and welcoming of other points of view, and your assessments are unbiased. I'm impressed by this and I wonder how you came to this place, this attitude, this frame of mind; I wonder, what was it like for you when you were a young intellectual and what was it like the development of your sensibilities; for instance, were you a loner? And at what point did the mathematician and the artist come together (which came first?); was there some sort of breakthrough or crisis or realization; I know that you were doing conceptual sculpture and painting and a sort of manipulated photography, did all this have anything to do with your turn to mathematical poetry? And, notwithstanding all your college education, do you consider yourself autodidact?

Kaz Maslanka:

“I want to say you are maybe the most intellectually generous person I have ever met; you are both aware and welcoming of other points of view, and your assessments are unbiased. I'm impressed by this and I wonder how you came to this place, this attitude, this frame of mind; I wonder, what was it like for you when you were a young intellectual and what was it like the development of your sensibilities; for instance, were you a loner?” That is a wonderful complement, although I find it hard to accept. I feel I have plenty of room to grow and can be less than generous in a couple of areas that come to my mind. However, I can talk briefly about my early environment and the first time I had a passion for knowledge.

As a child, I felt I was quite normal and related well with the children in my surroundings. (I was not a loner) It seemed to me that I was a bit goofy and always tried too hard to get a laugh. There were plenty of children in my area with which to make friends. I grew up during the late 50's through the early 70's in a white lower middle class "guns and Jesus" neighborhood typical of west Tulsa, Oklahoma . This part of town promoted the fad of decorating the front yards of their homes by posting bible verses on signs. These signs were about the same size as normal real estate “for sale” signs. There also seemed to be some sort of social hierarchy related to which families appeared to be the most righteous. Therefore, as fate would have it, I lived in a very religious part of a Bible belt city and had no idea of any other culture other than what little I could absorb from early sitcoms on the television. My parents never went to a university and three of my grandparents never made it to high school. Yet I must say to their benefit, they all possessed a certain kind of wisdom embodied in love. My father was the son of a sensitive, warm-hearted office clerk and a petite yet hot-tempered schoolteacher who chipped out their living in a small oil patch town in the Osage Indian territory of Oklahoma . My mother grew up on a wheat farm in a Kansas Mennonite community sharing duties with 5 brothers and a sister. Her father had a passion for technology even though there was not much around. He was the first in their town to have a radio and was always experimenting with antennas. My mother is an artist, three of her brothers, her sister and her mother were artists as well. My grandmother would paint whenever she could get away from the duties of the farm.

During my childhood, my father groomed me to be an engineer by feeding me toys in which I was able to build and create things. I gravitated to the Erector Set, Lincoln Logs, Tinker Toys and many others, some, which included electronics and electricity. My first cerebral challenge came after falling in love with the aesthetics of technology at age 12. I studied very hard to receive my ham radio license at the age of 14. I was fascinated with the invisible radio wave and the incomprehensible speed at which it traveled and how it bounced off the ionosphere 250 miles above the surface of our planet. Furthermore, I marveled at how radio waves were the same thing as light waves only at a different wavelength. For a boy whose traveling experience was limited to a small farming community in Kansas, trekking across the firmament by radio wave was very exciting. The mysterious and mystical fascinated me then and continues to fascinate me now.

The idea of becoming an engineer may have been an option however; at age fifteen I had a bad math teacher who jaded me against “word problems” which is now is the area of math that I love most. Therefore, to the dismay of my father, I lost interest in the idea of being an engineer and refocused on sports. Later on, my attitude became such that I exclaimed, “What is this math-shit for; I will never use it, for I am an artist!” As a result, my rebellious nature paved the way to me failing mathematics in high school.

On another note, I was fortunate enough that my high school art teacher exposed me to Dali, Magritte, Ernst and other surrealist imagery. It was at that moment the Muses entered my psyche and it has been servitude every since. It was as if Pandora's Box was opened exposing me to not only a dark side of myself but to a deity that was bound by the chains of the church. I still struggle today trying to understand the relationship of this deity to my artwork and myself.

In 1973 I received a track scholarship and experienced my first two years of college in Chanute Kansas at least 100 miles from any good library. It was hard for me to get information on Avant-guard topics and I had to have books shipped in from other cities. At the time my father controlled the finances and demanded that I not major in art for he wanted me to be an engineer. I convinced him that engineering would not happen so he pushed me in every other respectable direction trying to prepare me for the responsibilities of family and finance. I, like many artists, fought tooth and nail and wound up losing his financial support, which forced me into the long path. I worked my way through twenty-two consecutive semesters (eleven years) before becoming ill with panic disorder in 1984 and dropping out of school. I did get a BFA in sculpture (1980) but never realized my desire for a degree in physics.

In 1975 I moved to Wichita Kansas to enroll in the art program at Wichita State University . It had a very conservative art school however, I found three professors who kept my fire stoked. Stockton Garver was well versed in the mysteries of ancient art to which he served as a historian at the school. He was kind enough to allow me many wonderful conversations, which kept me energized in my efforts to study visual language and its relationship to my interests in synesthesia. I also studied music with Arthur Wolff who helped open my mind by expanding my understanding of John Cage and indeterminate systems for art. However, the man who influenced me the most and still influences me is the international art critic and aesthetician Robert C. Morgan.

Professor Morgan exposed me to a vast number of ideas concerning contemporary art, for he is a virtual encyclopedia of contemporary art criticism, aesthetics, and history. Professor Morgan just finished his PhD from NYU and (fortunately for me) landed a position in Wichita. I remember him executing a piece of art in which he described his location as being “In the vicinity of Dodge City ”. While at his apartment one day, he offered me some pita bread and cappuccino. I still remember the look on his face and his exclamation that I was “such a hick” when I told him I did not know what he was talking about. Although, I must say, that cuisine was not the most important thing Professor Morgan exposed me to--the most important thing was the ideas of conceptual art and a non-visual aesthetic. In retrospect, the two people he exposed me to that helped change the direction of my work were Robert Barry and Benar Venet. Both of these artists presented scientific or mathematical aesthetics in the context of art, which helped blur the line between the aesthetics of art and mathematics.

You mentioned my earlier paintings, sculpture, and wondered what relationship it had with mathematical poetry. The earlier work was more about trying to understand the nature of my synesthesia. I was trying to understand the transformation of an aural experience into a visual language. I guess I always was fascinated with polyaesthetics even if I did not have a name for it. However, I really did not get interested in using math as a language for art until 1979 when I had read the book, The Dancing Wu Li Masters, by Gary Zukav. It was a book about “the new physics” such as quantum mechanics, Einstein's theories, the nature of light, subatomic particles and physics' new relationship to eastern philosophy. The book seemed to me to be an expression of “Apollinairean surrealism” disguised as science. I knew at that time I had to dispose of my distance, disinterest in math, and start all over at the beginning for it seemed physics was as mysterious as anything I had experienced. My interests seemed to have a seamless transition as I started classes in math and physics and finished the requirements for my BFA in sculpture. While I was studying math it dawned on me that the variables in an equation could represent anything that I wanted for it was an empty box with an unknown inside. It was an exciting realization however; I did not know it would be the direction that my life would follow. It then followed that mathematics could be used to describe how I perceived motion in an image such as Kandinsky's Composition V. Kandinsky's work gave me the ideas for the Psychovector Series (1981).

“Composition V,” Wassily Kandinsky (1911)

“Equal Momentum, Seven Times The Difference In Velocity,” Kaz Maslanka (1981)

I began to bounce some of my ideas off Professor Morgan however, unfortunately for me, he decided to take a teaching position back in New York . I felt virtually alone, stuck in Kansas, with no immediate artists to share my interests in using math as a language for art. Between 1981 and 1984 I created my psychovector series--equations used to measure visual kinematics in a static image. Although the conceptual part of the work was done by 1984 and due to my perception that no one would be interested in the work, I waited to 1988 to finish executing all the canvases. As a result the canvases are dated 1981 to 1988.

I bought my first computer in 1979 and my first mathematical poem, titled, “Psychronometrics,” was created in 1983. It was an interactive computer program written for the radio shack “color computer” and possibly might be my best work to date. I also wrote a handful of other mathematical poems between 1983 and 1986. In 1984, I became very ill and began hating the curse of being an artist. I suffered for five years before I was able to think seriously about doing any art again. Furthermore, the following 10 years were a healing period where I decided to study music and distance myself from visual art, even though the mathematical poetry and polyaesthetics were always tugging in the background of my mind.

My illness destroyed what academic career I had and forced me to address spiritual concerns. In retrospect, I can see from 1973 to 1989 I unknowingly ran from my inner self and from the inconsistencies and egos that I found in the church. In 1989 I embarked on a spiritual path that demanded logical explanations for all of my questions concerning the transcendent and fortunately I found what I needed in the work of Joseph Campbell.

Concerning your question of being an autodidact -- I continue to study as much as I can however; I feel my technical abilities as a visual artist have been suffering as of late. I hope to put more effort in that area soon. It is very difficult to be good in “polyaesthetics” or many aesthetic endeavors. As well as what you know, I guess I should also mention that my tenuous efforts are not just expended on the later but I also struggle as a musician however, it is my lowest priority. To answer your question, the bottom line is that I would have to say yes, I am an autodidact not only in my artwork but in my “day gig” as well.

In 1984, I got a job as a file clerk in an aerospace engineering department running blueprints and filing the engineering drawings in the vault. I took the job in hope of learning engineering so that I may have some way to make money to support my art and possibly go back to school to finish the physics degree that I had started. I worked fast to finish my clerk duties so that I could beg the manager for time in the design room. From there I was able to teach myself to design on the drafting table. I achieved the point where I was designing quite well however, the manger had no intention of making me a design engineer for he had hired me as a file clerk. Fortunately, after some time, they promoted the manager to another position and after seeing my engineering design abilities, the ensuing new manager, being a bit confused, asked me why I was working in the vault. I said, “I don't know, you tell me.” At that point, he moved me to be a designer and thus started my current consulting career as an aerospace engineer.

GVST:

The idea of words acting as numbers do. Would you explain how you conceive of this (of just how this is possible--or are we, must we, be given to speaking analogically here); and also, while the words are acting mathematically (if that is indeed the case), are those heretofore strictly mathematical operations now given to acting grammatically (in co-operation, or synesthetically), or does this aspect, or, operation, of the equation remain strictly mathematical (as it seems the mathematics is the vehicle, the carrier-forth, of the poetry). And: It seems to me, that in your conversion of words into terms that are available mathematically, a general rule that you follow is to find an intermediate sense, a middle ground (a matter of “magnitudes,” say); and further, that your words are considered not according to sound or orthography, but strictly according to their signification. . . .

Kaz Maslanka:

I'm going to break your question into three parts--the first will address the idea of words as number, the second being the relationship of mathematical poetry to grammar, and the third part being some criteria that may be used to critique mathematical poetry.

First, mathematics among other things is a formal language. The mechanics of mathematics for mathematical poetry is no different from its mechanics with science or economics other than we use the equations for connotation as opposed to denotation. There is nothing mystical about how mathematical poetry functions with math however, it may seem mystical to those who do not know how to use math as a language and have no experience using applied mathematics. It also may seem mysterious to those who know mathematics but have no experience with poetics. Words acting like numbers are consistent throughout all applications of mathematics although most people do not think in those terms. In an application of mathematics, the meaning of the words has magnitude or value and the value can be expressed as a number. Anyone who has taken an algebra class has encountered the challenge of “word problems” furthermore, when we talk about the field of “applied mathematics” we are really talking about the vast expressions known as “Word problems.” Applied mathematics is the backbone of many academic endeavors including statistics, physics, engineering, chemistry and accounting. In the application of mathematical poetry, it is the relationships between the concepts in the equation, which form our interest as opposed to an interest in number. As an example, we may ask Bob how he is feeling and Bob says, “I am feeling better than yesterday.” You can easily see that we do not have to have a number telling us that Bob is 15.5647 percent better than yesterday to have a meaningful understanding of what Bob has experienced. What is important to us in our search for meaning is the relationship of yesterday relative to today. Within the scope of mathematical poetry, the “mathematical equations” provide us with relationships so that we may interpret meaning.

This brings something else to mind; it may be fun to answer the opposite of your question. Let us look at using number as metaphor. What is important in this case is that the units for the number would indicate the number's identity as a metaphor. I see numbers without units capable of being symbolic but not metaphoric. Of course, within the context of mathematical poetry the units would be a direct reflection of the words in the poetic equation for the words/concepts in the poem dictate the units. I must mention that I have done very little of this type of poetics furthermore, I have not seen anyone else approach it as well. Admittedly, there is a lot of room here to explore. A good example of numbers being used as metaphor would be my “Psycho-vector” series and “Psychronometrics” my first and only computer interactive mathematical poem.

Second, there has been much written by cognitive scientists and linguists concerning the descriptive grammatical aspects of mathematics. Mathematics has always been used for denotation within the numerous fields of applied mathematics. The focus of mathematical poetry is to use the language of mathematics for connotation focusing on the poetic aspects of metaphor as well as providing what I call a “reflexive didactic,” which I will talk about a little later. While pure mathematics has no expression of metaphor, it does provide us with a structure for expressing it. Mathematical poetry points at the metaphor by gathering concepts from different sources and placing them within a single context. Let me first address metaphoric structure in a verbal metaphor. As an example of a verbal metaphor we could state, “The eternal sleep of death awaits us.” Here we are comparing the attributes of sleep to the attributes of death. I really like the cognitive scientist George Lakoff's terminology defining the different parts of a metaphor. Lakoff puts the metaphor in terms of a “target domain” and a “source domain.” The “target domain” is the subject to which attributes are ascribed. The “source domain” is the subject from which the attributes are borrowed. In this nomenclature, we describe metaphors using the convention “target IS source,” with the word “IS” always capitalized; in this notation, the metaphor that we just discussed would state that “death IS sleep.” The semantic tension created in a metaphor is due to the dissimilarities of the target and the source within the structure of the metaphor. What I find interesting about mathematical poetry is that a mathematical equation defines the target and source domains for metaphor. In the realm of mathematical poetry the equal sign “=” is substituted for the “IS” in the metaphoric structure. Therefore “a = b” translates as “a IS b” or “target IS source.”

Thirdly, it is interesting that you bring up synesthesia in this context. Before I talk about its influence in my work, I want to mention that synesthesia is supposed to be involuntary and not empirically based. I believe that empirical synesthesia exists and I have personally experienced both kinds. Futhermore, I believe there is a direct connection between the two, however I am speaking about empirically based synesthesia in this interview. I believe synesthesia has played a major role in developing my mathematical poetry and it may play a role for others as well. Furthermore, synesthesia is the semantic glue of polyaesthetics. I see human experience as a combination of sensory information filtered through all of our senses. Furthermore, I see the meaning of the experience being established in relation to all of our past experiences. Intuitively, it seems as if meaning is established by the context of the experience, which is built from a massive hyper-dimensional verbogeometric vector sum. I believe that once a poet/artist has learned mathematics as a language they can experience phenomena and transform sensory experiences into the language of mathematics. I also have to mention that I do not see this later process being any different for the sciences than it is for mathematical poetry. However, the mathematical poet sees the physical phenomena as the source domain for potential metaphors as opposed to something that needs linguistic correlation. The mathematical poetic aesthetic relies on creating the metaphor with the target domain that provides a didactic which points to elements of the human condition. I find the more mysterious the elements the more beautiful. This later concept is what I call “reflexive didactic” which is an aesthetic that should be judged by how well the mathematical statement reflects a question. The aesthetics of mathematical poetry lie in the beauty of how well the question relates to the experience of life. I see this experience being a full spectrum from realizations in understanding ones spiritual identity to purely base hedonistic sensual pleasures. The range of experience and subject matter for mathematical poetry is the same as that for any of the arts.

GVST:

I'd like you, please, to address some of the considerations to do with the interpretation of mathematical poetry, such as, and especially, the role played by paraphrase. I find as I strive to articulate my concerns for you here, I come to wonder if it might not be appropriate to state the issue as “the problem of interpretation in mathematical poetry,” and/or “the problem of paraphrase in mathematical poetry.” And this is because, first of all, it seems in the appreciation of mathematical poetry that we are given to translation from one language (being that of math) into another (say, English), and it seems my appreciation of the math poem, or more specifically of the poetry of the math poem, is in that English translation, and the math is just something I need to ford--I wonder if the math, instead of being revelatory of the poetic, does not in effect act as an occlusion, a code that I must first crack before I gain access to the poetry. And it seems to me that that translation, that passage into the poetry, while perhaps an experience of the poetic, is nonetheless an experience via paraphrase--the result of a string of intellection, and not an immediate intuition. Further more, it seems to me the mathematical poem has a dual structure--it seems that what the mathematical poem presents is a picture, and that has one structure, a dramatic structure, if you will, while the poetry, which I must translate my way into, has another structure entirely, and that being a logical structure. I guess I can state my concern this way, and this leads into the second part of my question: Where lies the essence of the mathematical poem--is it in the picture, is it in the paraphrase. . . ? And, finally, “polyaesthetics.” As this seems to serve as the foundation of your aesthetic, would you explain, please, your use of this term, such as to how you conceive of this and its break down or organization into constituent parts; and, also, as you speak of “the aesthetics of mathematical poetry” and that “the mathematical poetic aesthetic relies on creating the metaphor,” would you say, please, where exactly in mathematics might we locate those elements that give us to speak of mathematics in aesthetic terms (Need we look no further than that equals sign?), for it seems we speak by analogy when we say such that this or that equation, or such that this or that characteristic of the equation, is “beautiful.” I wonder if we may not substitute the term affective for aesthetic? Can we isolate the specific values of mathematical poetry? I thank you so much for your time, Kaz Maslanka.

Kaz Maslanka:

I feel a little uncomfortable thinking in terms of interpretation. I can understand giving someone the tools to access a particular work of art, however I generally do not see the need for interpreting art/poetry. I can imagine that interpretation may be required for those who do not know how to “read” the mathematical or the poetic languages. In addition, an art critic of mathematical poetry may wish to help those unfamiliar with any of the languages or aesthetics used by the mathematical poetry. However, interpretation should only be used to help motivate the receiver of the artwork to, as you say, “ford” the difficulties and engage in learning mathematics as a language. On the other hand, an interpretation may possibly help a struggling mathematician gain insight to the nebulous truths that can only be enjoyed though metaphoric language. In that sense, the critic may paraphrase her/his experience to become tools to help the percipient achieve the aesthetic in question. The bottom line is that there is no “problem with paraphrasing” or “problem with interpreting” mathematical poetry. Paraphrasing and interpretation are aids needed only for those who do not know the language of mathematics and/or are not familiar with poetics. Learning mathematics as a language is no different than learning a second verbal language, for you start with memorizing and end up with it becoming second nature. I am not advocating a requirement of a PhD in mathematics to understand what I am expounding, for a single algebra class enriched with word problems will suffice. Furthermore, I think the idea we are reaching for is not paraphrase but paradigm. Yes, paradigm is the structure needed for mathematical poetic cognition. One has to “make sense” of what one is experiencing or it becomes meaningless garble. I feel it is important for a mathematical poem to be structurally tied to a paradigm where the poem serves as a mathematical model/object and yet functions as a metaphor. The structural paradigm provides the semantic voice for the reflexive didactic, which points outward posing questions and enabling the poem to resonate through multiple levels of language. In my blog, I have a section in the sidebar that displays a taxonomy for mathematical poetic structures. Within that list there is one technique called a paradigm poem.

What is a little misleading is that all of the structures listed in the taxonomy are really paradigms, however I see the paradigm poem being more blatant in its appropriation of a popular mathematical paradigm (model) currently used in applied mathematics. The point I am trying to make is that the poem should have a paradigm to help hold everything together. To make an example lets look at the mathematical poem “Monocular Mistress”: Granddaughter of Uranus = (The bow of Artemis)(Ishtar's Gravity)/(The undulations of the moon).

Here we have a poem about the daughter of Cyclops expressing a mathematical relationship with all the terms in the poem. If the poem were not tied to the paradigm of similar triangles then it may seem to be gibberish.

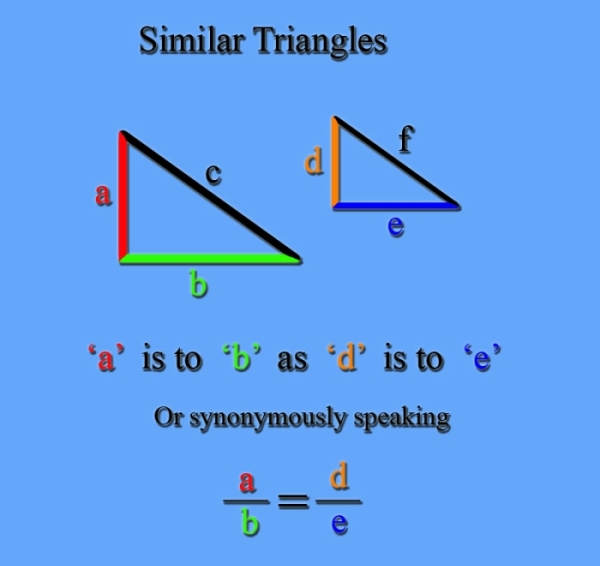
Similar triangles have the property that the length of a leg in the triangle divided by the length one of its adjacent legs is equal to the same division of corresponding legs in the other (similar) triangle. A diagram of this concept is much easier to visualize than the latter sentence and may be viewed in my blog or you can Google “similar triangle poems.” This principal is expressed algebraically as: a/b = d/e Or we can express it in words as: “a” is to “b” as “d” is to “e.” The poem can also be expressed as two different ratios by saying: The Granddaughter of Uranus is to the bow of Artemis as Ishtar's Gravity is to the undulations of the moon. Some people may say, “Well, why don't you just leave it expressed as words and forget this mathematical thing.” What that person would be missing is how it beautifully relates mathematically and linguistically to other similar triangle paradigms inspired by the natural world as well as the semantic kaleidoscope perceived when experiencing the syntactical permutations available in a mathematical poem. Furthermore, there is a mathematical aesthetic involved in mathematical poetry, which is tied to the historically rich global development of mathematics, and supplies a beauty that deepens the content of the poem much the same way that cultural and historical references function in language poetry. Of course, the more one understands the history and development of mathematics the richer is ones experience. As you say, there may be a string of intellection before you can get to the point of intuition; however, I see it no different from the string of intellection one struggles with learning in language poetry. One does not just jump right in and have an intuitive grasp of meter, metaphor, alliteration, culture, poetic history and the numerous other aspects of language poetry without some serious study.

It is so interesting that in your questions, you mention a dual structure. I think your perception is correct as far as one could view the mathematical poem as possessing dual structures; however, I see the poem having only one mathematical structure functioning two ways. First, there is the structural paradigm and then there is the metaphor created by the equal sign. If one views the paradigm as a metaphor, then one will experience a metaphor within a metaphor. To view the structural paradigm as a metaphor one would need to view the mathematical structure of the poem as the target domain and all the mathematically identical structures inspired from the natural world as the source domain. Therefore, the essence of the mathematical poem for which you are asking would exist in both functions, the first function being one of structure and the second being one of words.

Polyaesthetics is a term I use in connection with my artwork, as it embraces three different aesthetics--the aesthetics of verbal language, the aesthetics of visual language, and the aesthetics of mathematical language. I view all three aesthetics being poetic components in a polyaesthetic piece. Polyaesthetics provides an environment whereby one may have multiple metaphors nested inside each other as well as multiple metaphors synesthetically relating to one another. If one looks at the context of the entire piece as the source domain and all of the concepts presented as the target domain then the entire polyaesthetic piece is a synesthetic poetic expression. It is synesthetic due to the linguistic dissimilarities in the multiple aesthetics employed. It is such that verbal metaphors presented with mathematical paradigms, which point to other structures in nature, tie themselves into the visual metaphors mixed into a synergetic sensory experience. I feel the challenge is to balance all of the semantics to create a meaningful experience.

The question of locating the mathematical aesthetic in the field of mathematics is as vast and nebulous as asking for the location of the art aesthetic in the field of art. The aesthetics of mathematics is as deep and expansive as to limit itself only by the boundaries of the mind itself. I do not consider myself a mathematician so I am extremely limited in scope for discussing the depth of mathematical aesthetics. However, I can talk about the mathematical aesthetics that I find fascinating as well as those being related to mathematical poetry.

I really struggle to find a metaphor suitable to express the clarity of mathematics. There is nothing more precise and clear, as that of a mathematical expression. For mathematics is the definitive of clarity, there is nothing the mind can conceive with more purity and precision. The beauty in this clarity is sublime showing itself as the structure of our thought process as we relate one concept to another. Due to this clarity, math is the perfect language for the human mind to correlate experience and we see this manifest in the numerous disciplines of applied mathematics. This same beauty in correlation is present in mathematical poetry by employing the aforementioned structural paradigm. Mathematics not only displays beauty in its applications in the natural world it also shows beauty within the mathematics domain itself. As an example, many people point to Euler's formula as the most beautiful equation in the discipline of mathematics. This equation usually shows a relationship between the ideas of the natural log, complex numbers, the transcendental number of pi, the idea of one, and the idea of zero. (In some examples of the formula, the concept of pi is excluded).

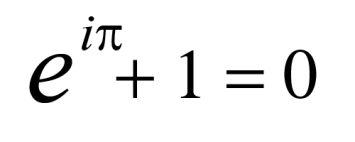
There is also a mind boggling magical property within the realm of mathematics. Among many things, mathematics is a system, which enables us to relate symbols to each other in a vast variety of syntactical forms that still function with correct logic. This system provides us with problem solving ammunition to conquer the most complex of ideas. If one could see all of the mathematics involved to display this interview on ones personal computer then one would experience a multitude of wonders in the ability of humans to construct something so logically complex and yet viable. Even simple mathematical problems can seem truly magical in their ability to deliver our expectations. I do not feel I have the space here in this interview to fully illuminate the mechanics of the collaborative substitution poem so it would be best if one follows the link to understand how it works. However, I do wish to make the point that the collaborative substitution poem is a good example of how mathematical poetry uses the system of mathematics. This beautiful system provides numerous syntactical formations, which enable us to manipulate multiple poems into one cohesive mathematical poem. In addition, these permutations are analogous to playing a piece of music in different keys to experience subtle variations of sonic qualities, whereas in our poem we have different permutations to experience different semantic variations. Yet in the music, the relationship of the notes remains the same and in our poem, the logic remains the same. Furthermore, the collaborative substitution poem also has the ability to grow indefinitely over time as other mathematical poets substitute terms in the existing poem with poems of their own creation.

To answer your last question -- you seem to be asking about the relationship of the words aesthetic and affective. I see the word aesthetic being a class or category, and the word affective being a functioning constituent of the aesthetic class. Furthermore, when we talk about a particular aesthetic feeling, I feel we are pointing to both the class and the affective sensation.